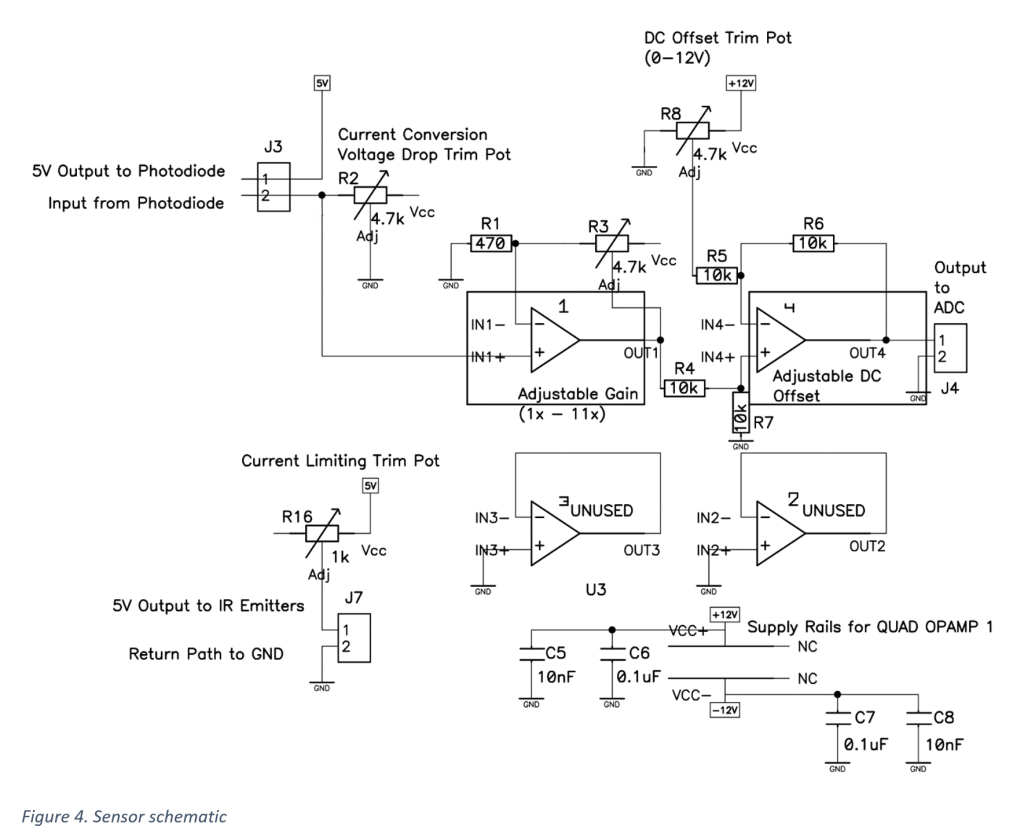
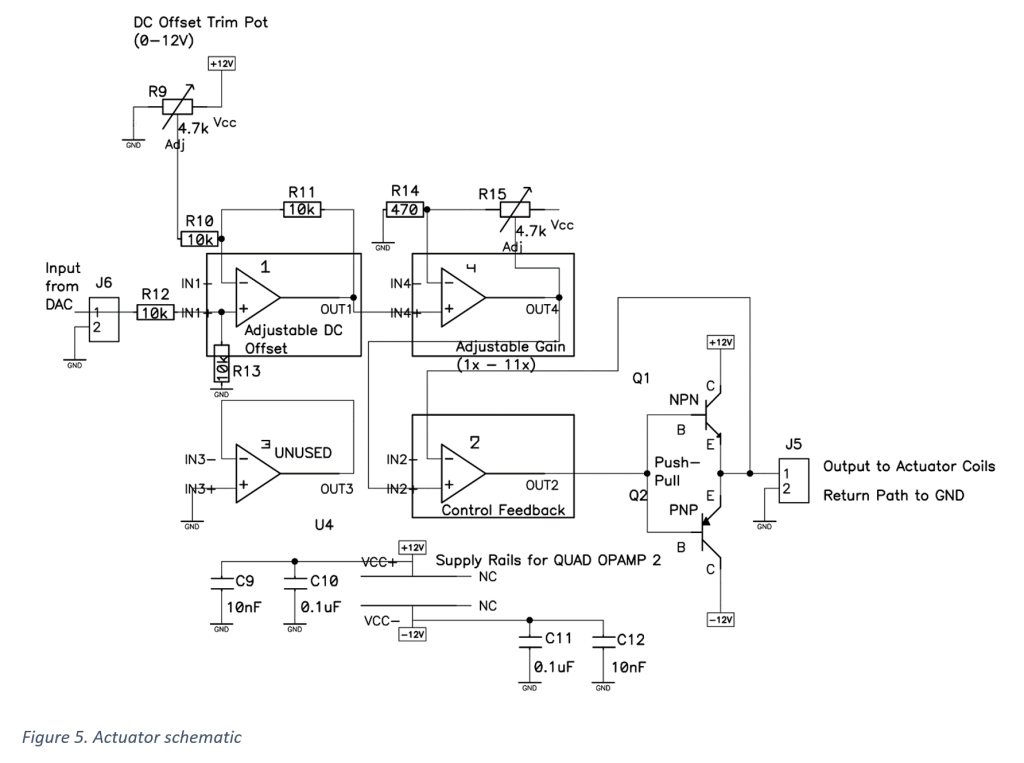
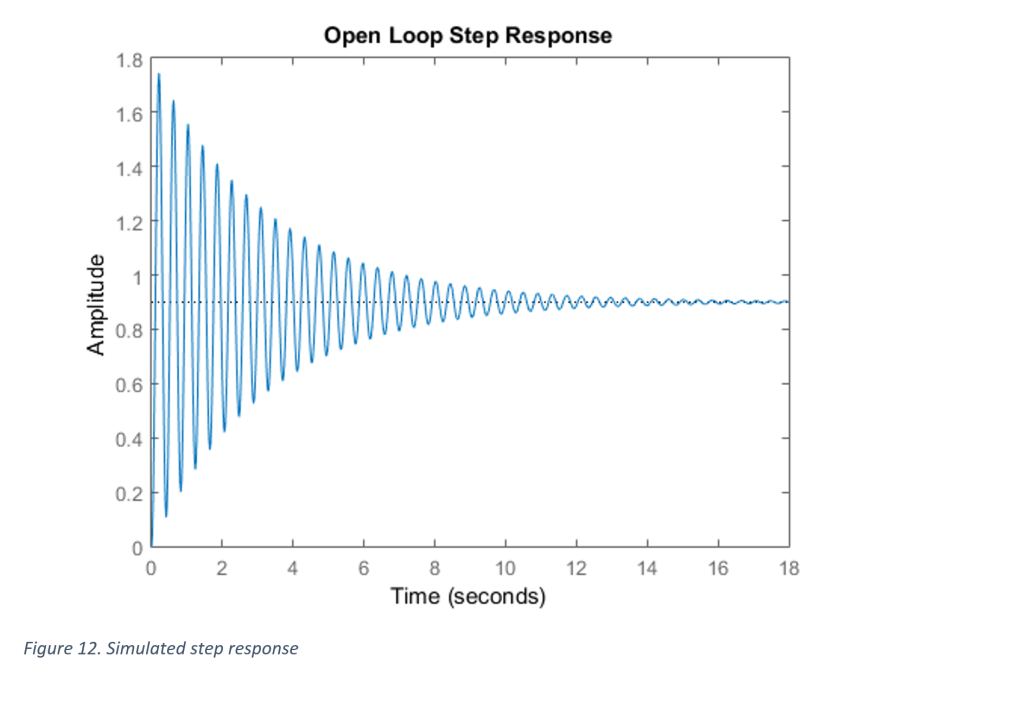
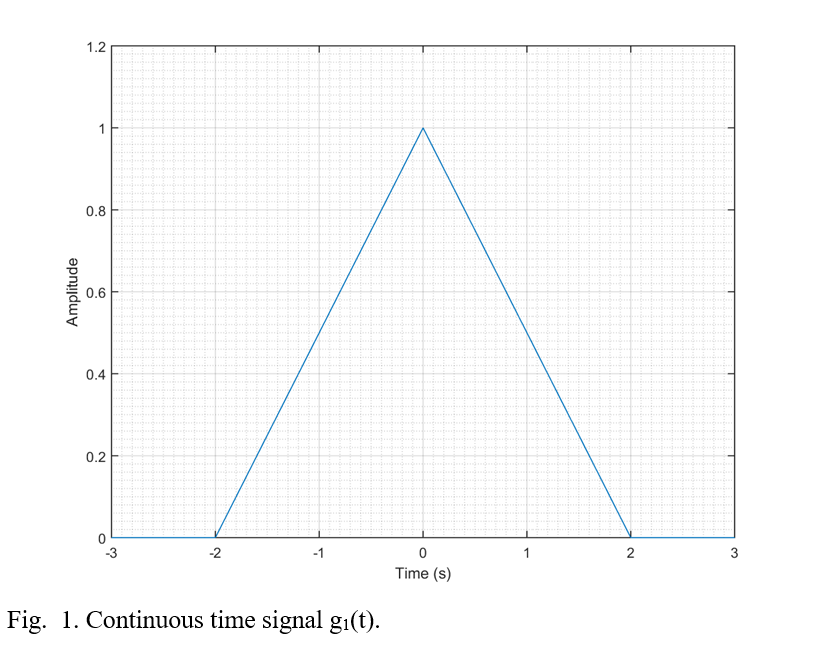
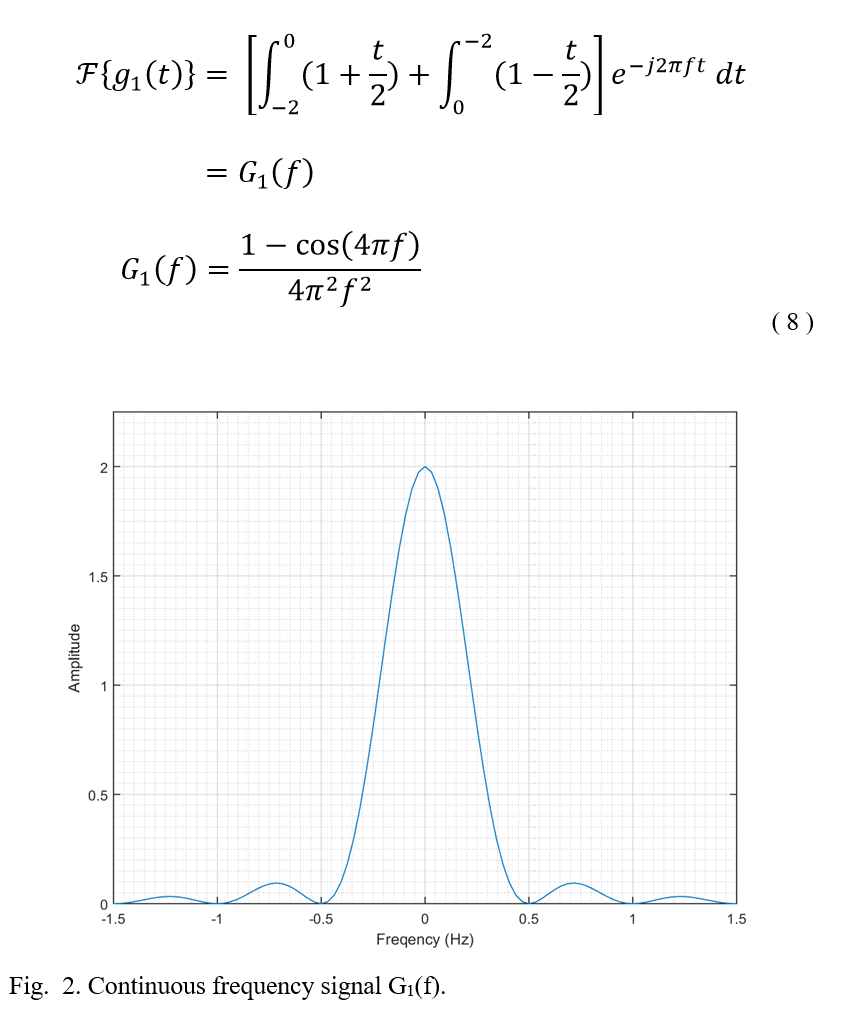
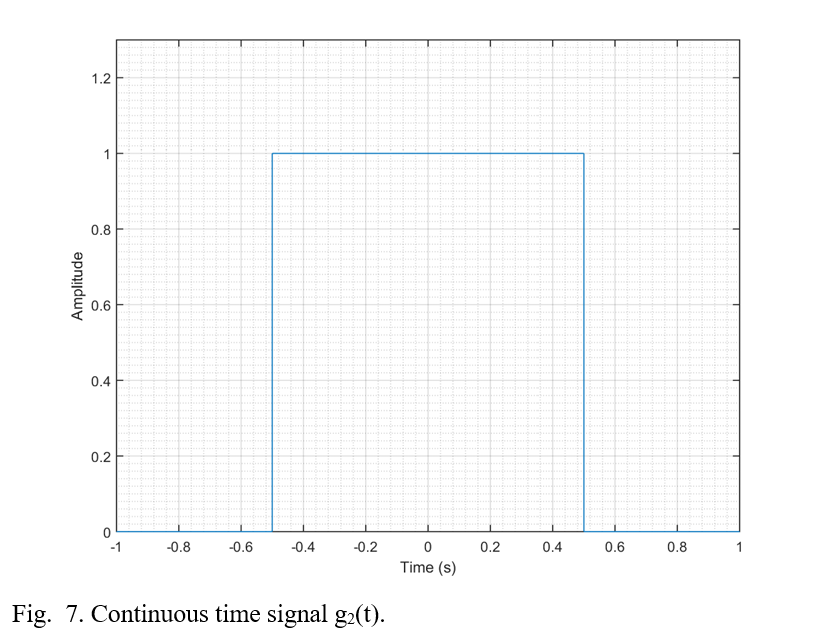
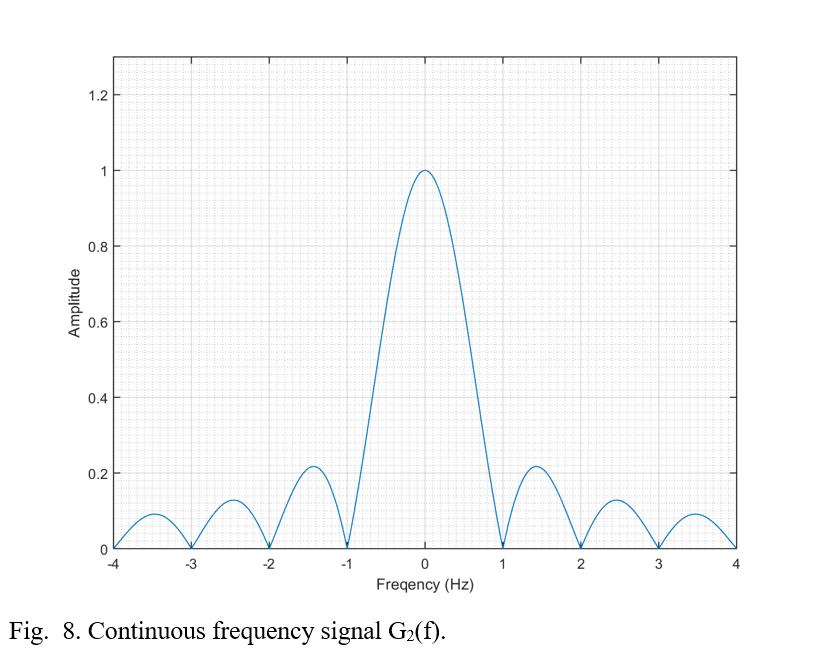
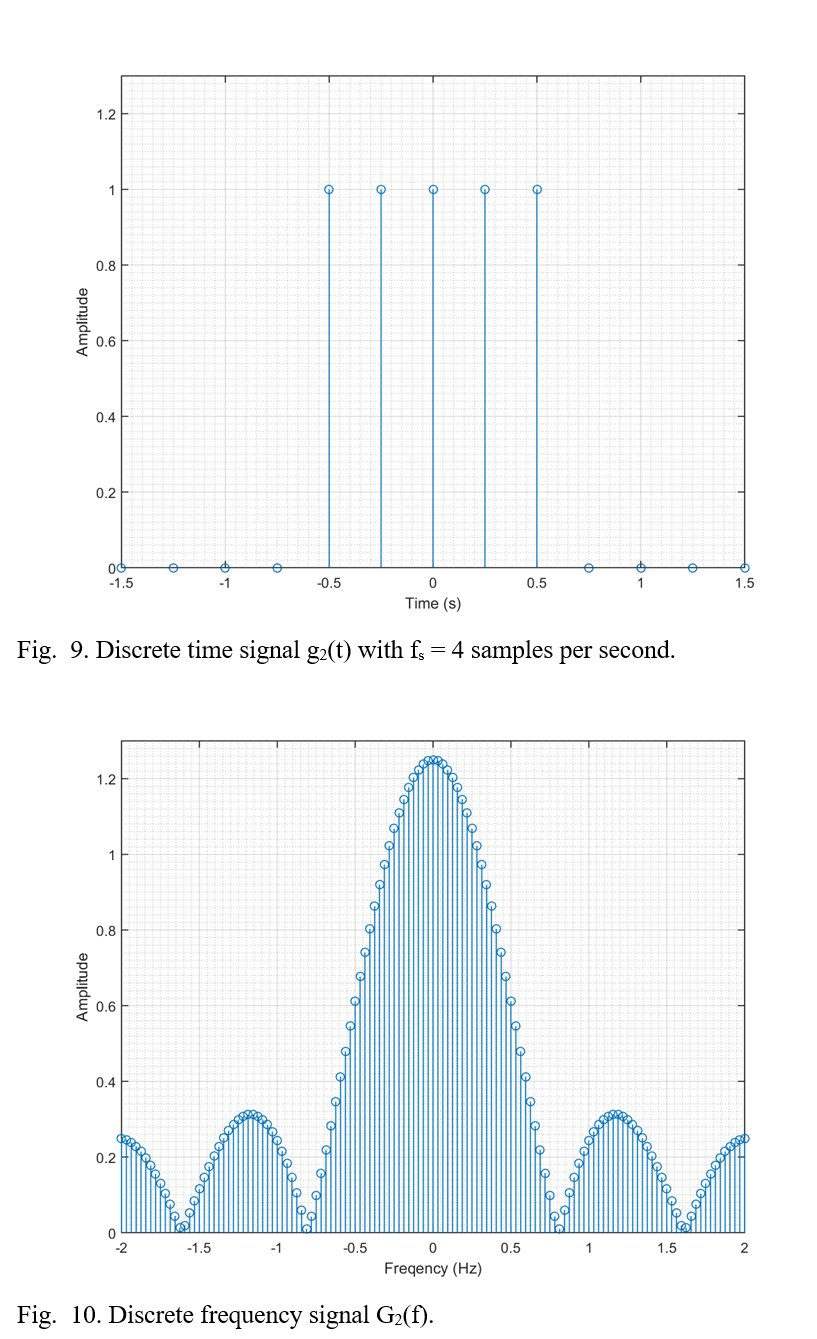
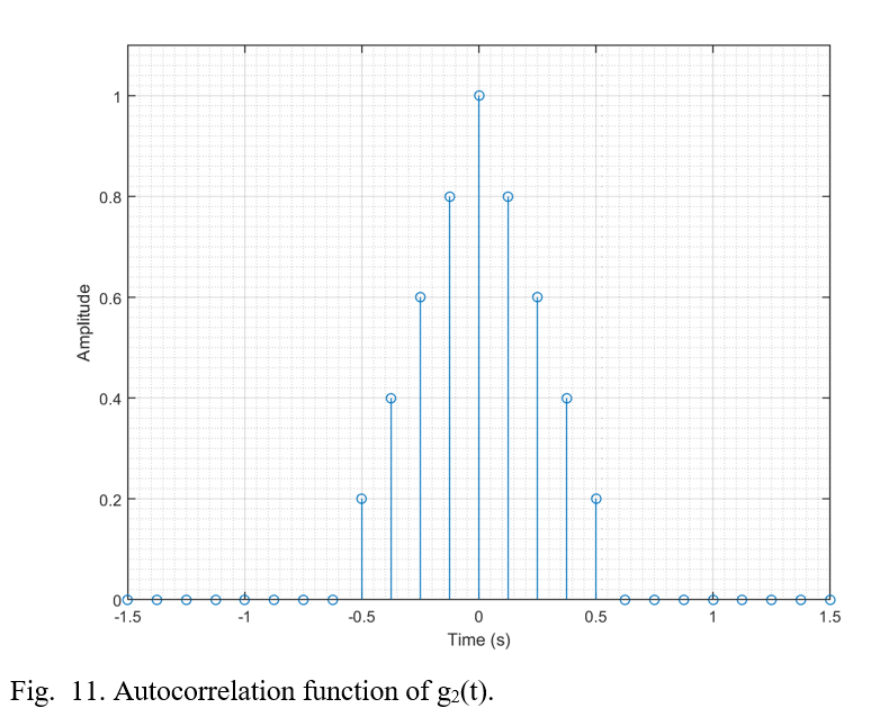
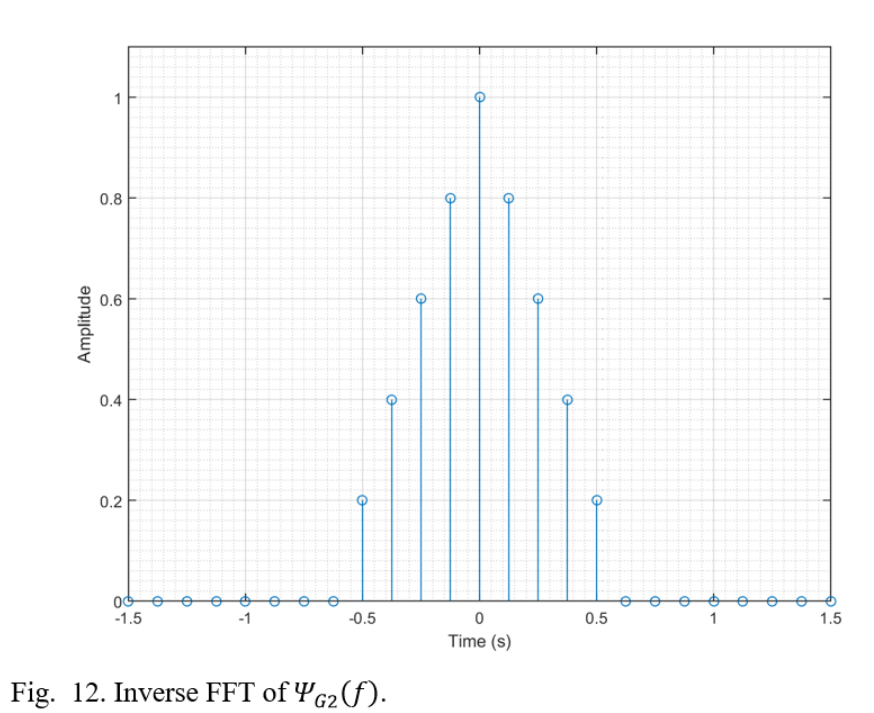
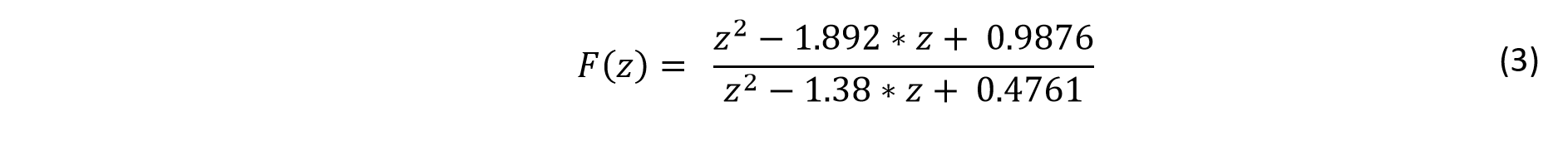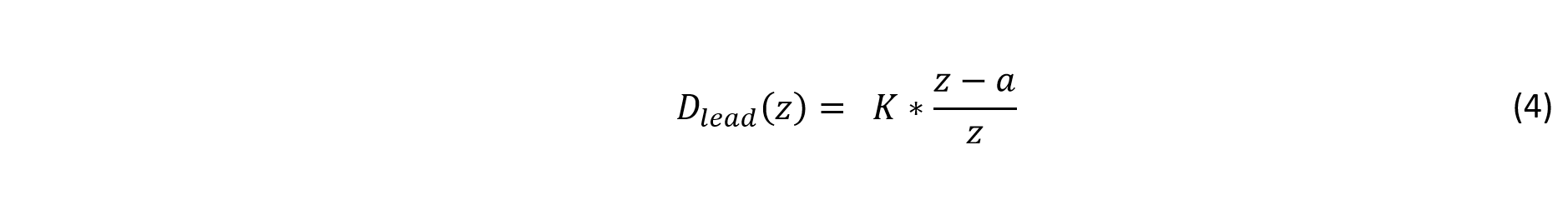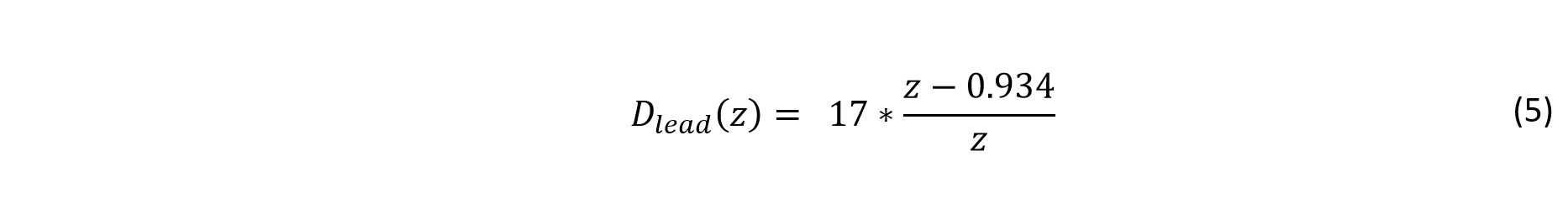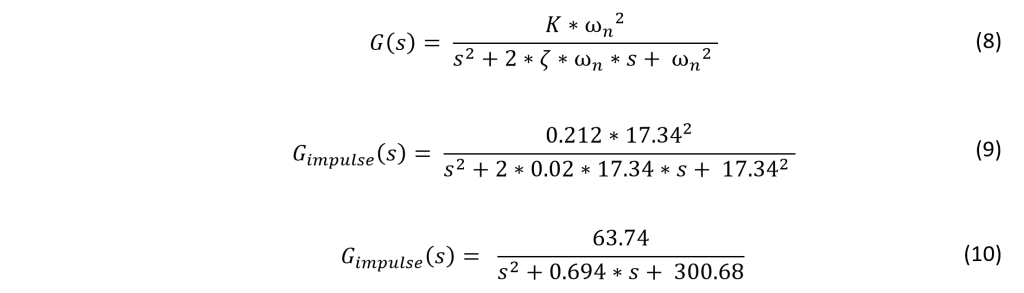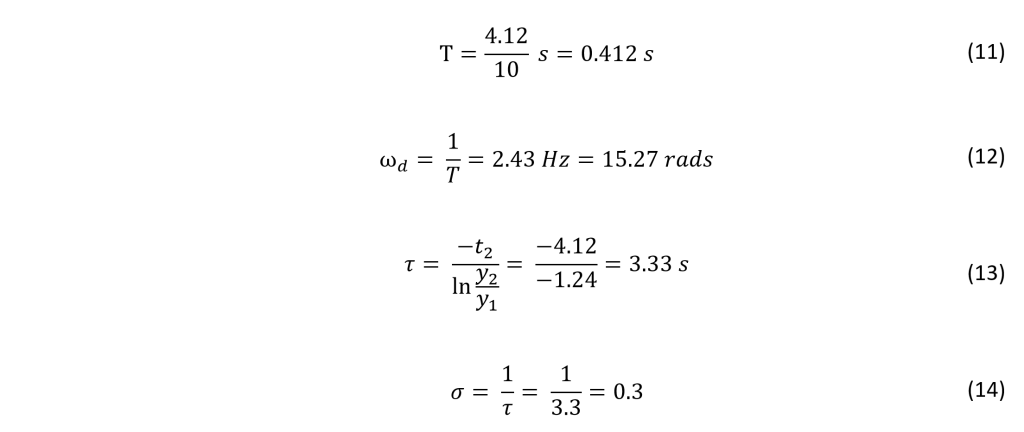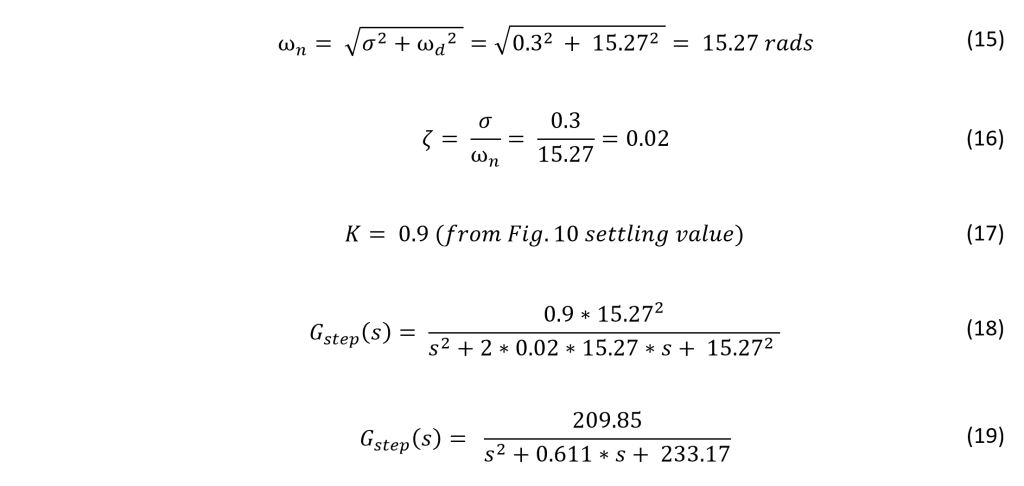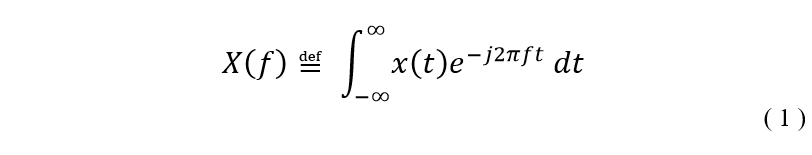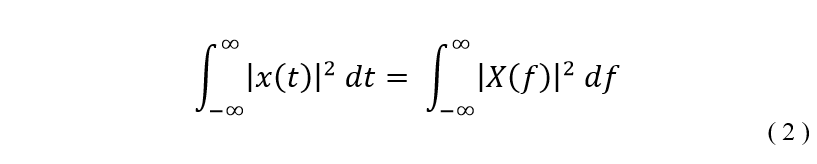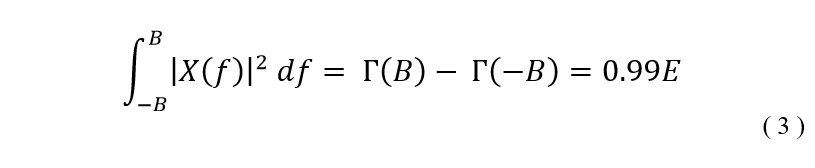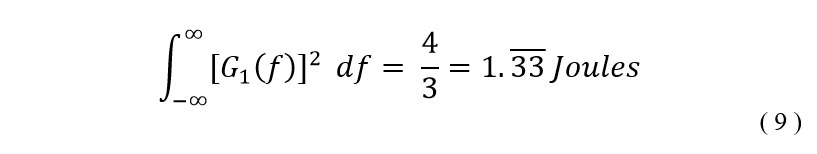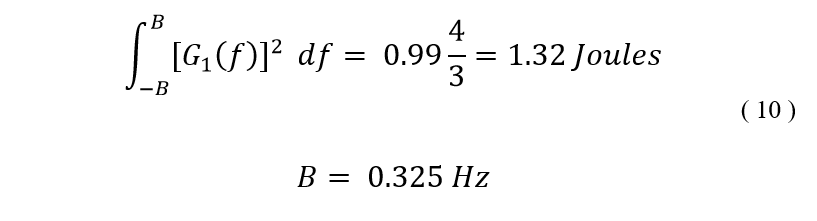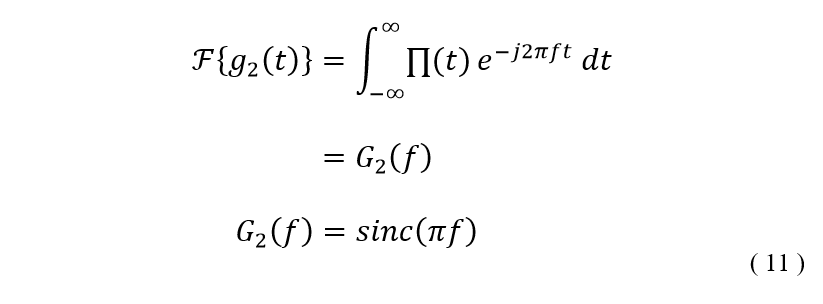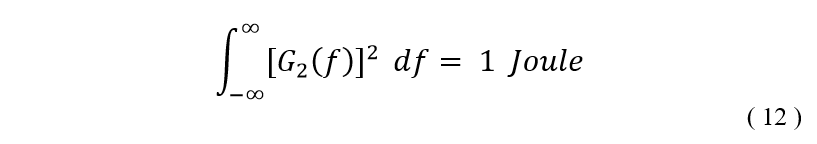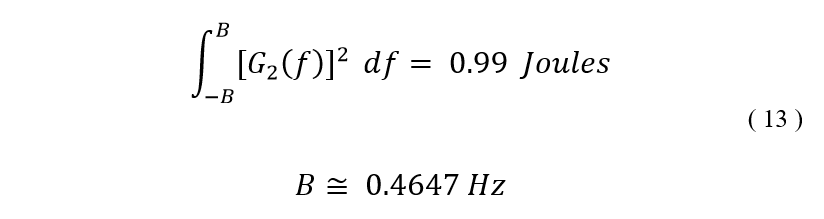All posts by Zack Goyetche

Chemistry Stir Plate

January 1, 2016 Zack Goyetche 4 Comments

Recently I came across an old chemistry lab stir plate made by Fisher. I thought it would be a fun weekend project to restore it and add some functionality. Here’s a before and after shot of the project.

Keep scrolling down if you’re interested in more detail!

In addition to restoring the paint, the features that I added are as follows:

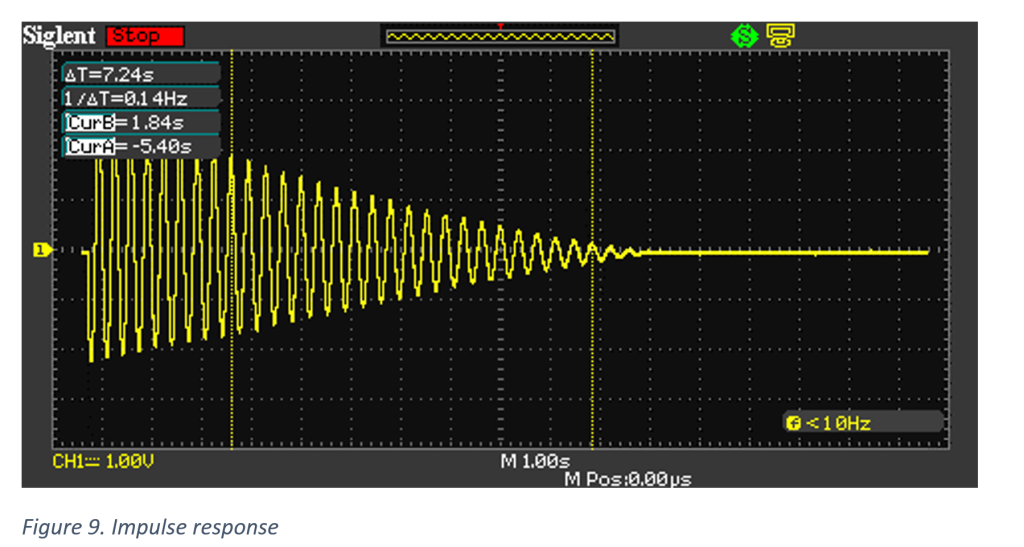
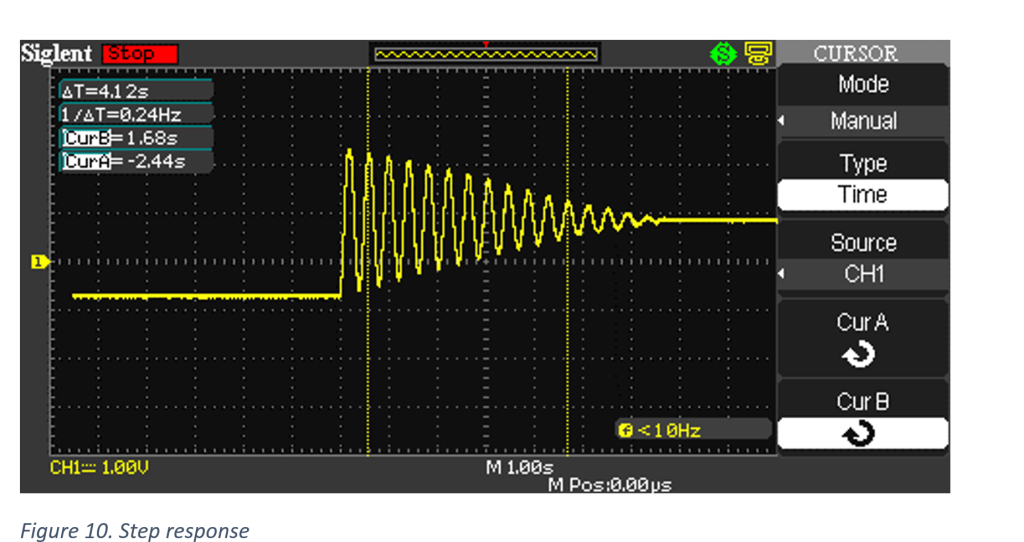
Adjustable speed (5 to 150 RPM)
Adjustable direction
User interface (LCD + Rotary Encoder + Piezo Buzzer)
K-Type Thermocouple for temperature readings (-200 to 500°C)
Shake mode
Stir mode

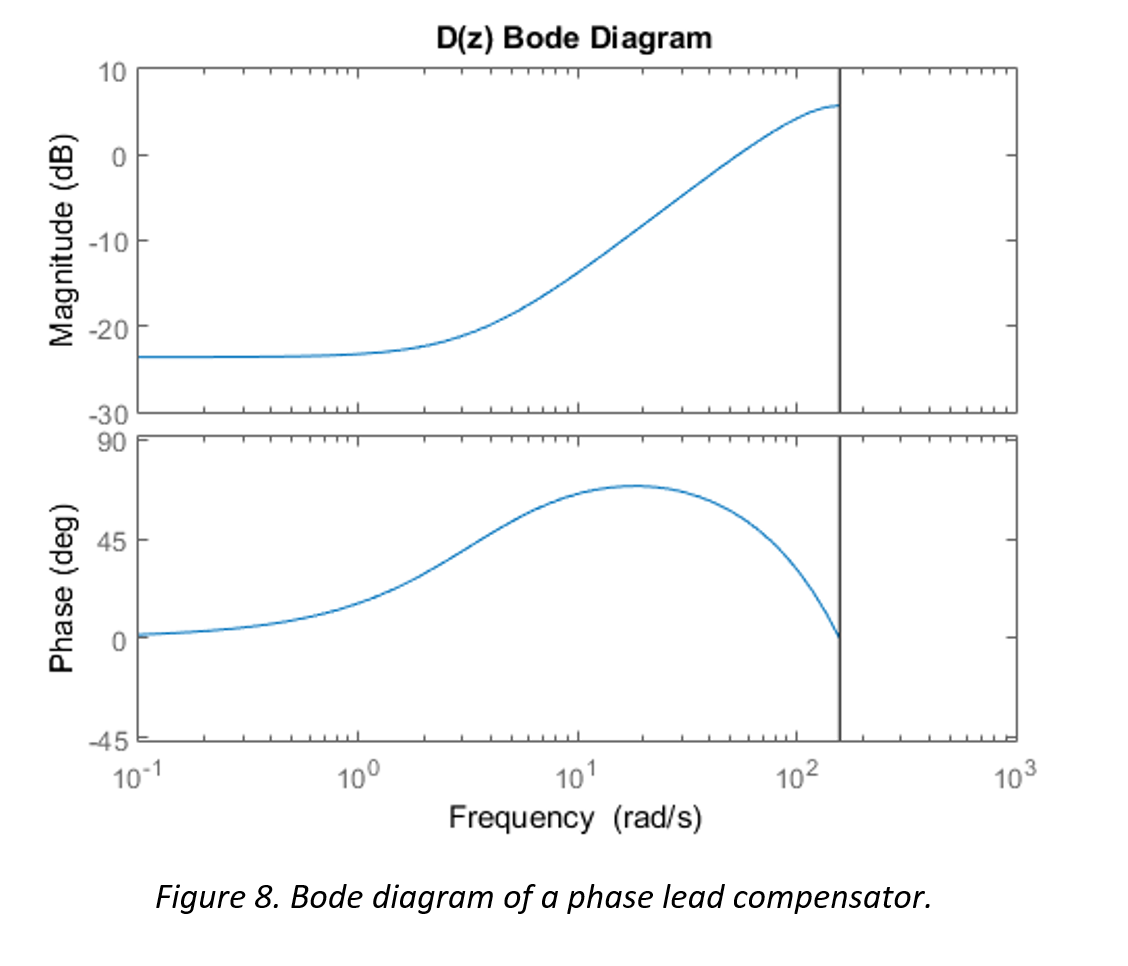
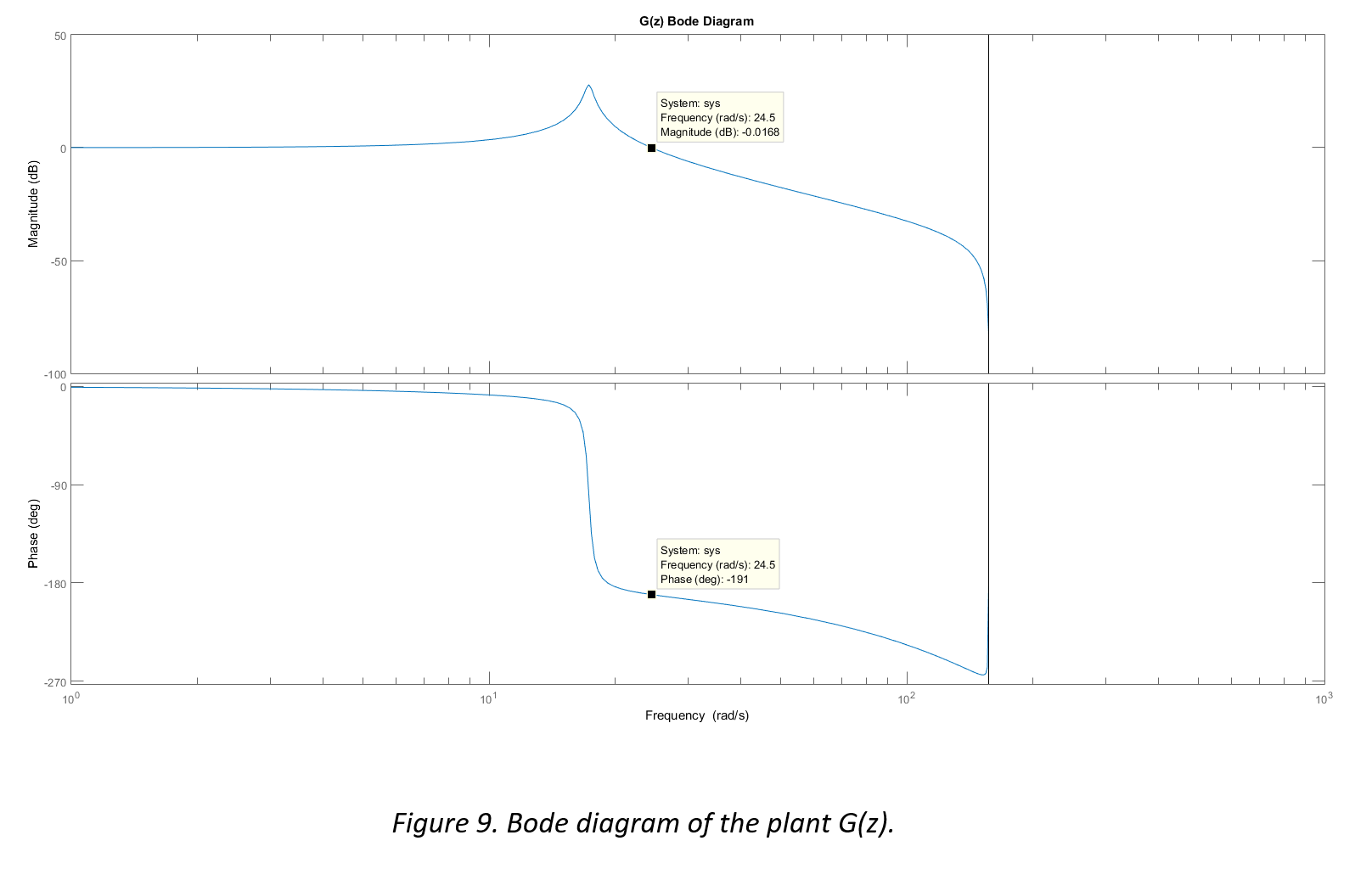
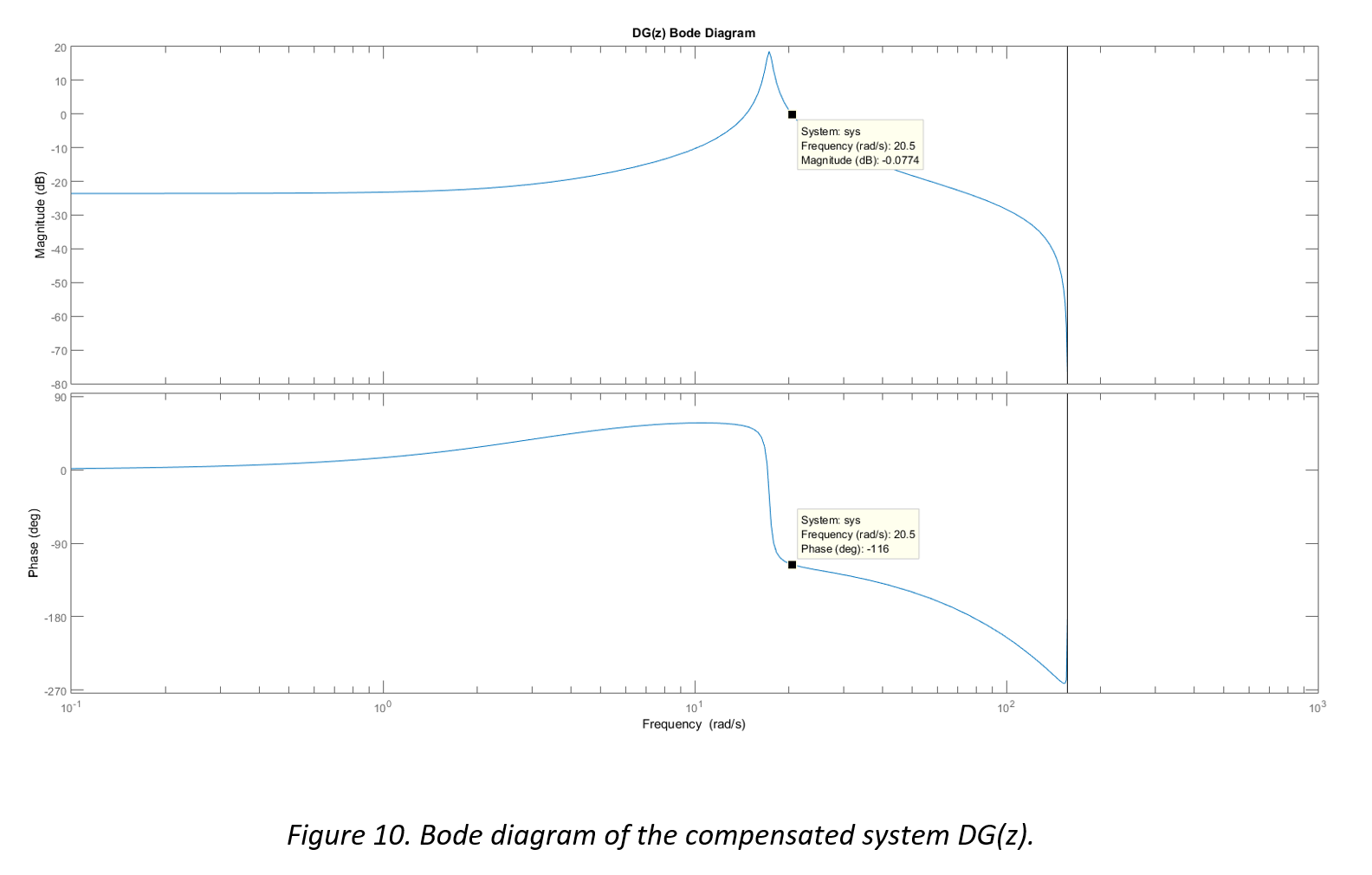
The microcontroller used in this project is a 16-bit PIC24FJ64GA002.
The C code written for this project can be seen here.

Case

The stripping process:

After the case was clear of old paint and debris, I dremeled out the face plate to make room for the LCD and a switch. I used the hole that was already there for the rotary encoder. Additionally, I cut a port out in the back so that I could add a fused switch for the AC connection.

Finally, I rinsed the case in mineral spirits, applied a primer coat, and then the paint.

Motor

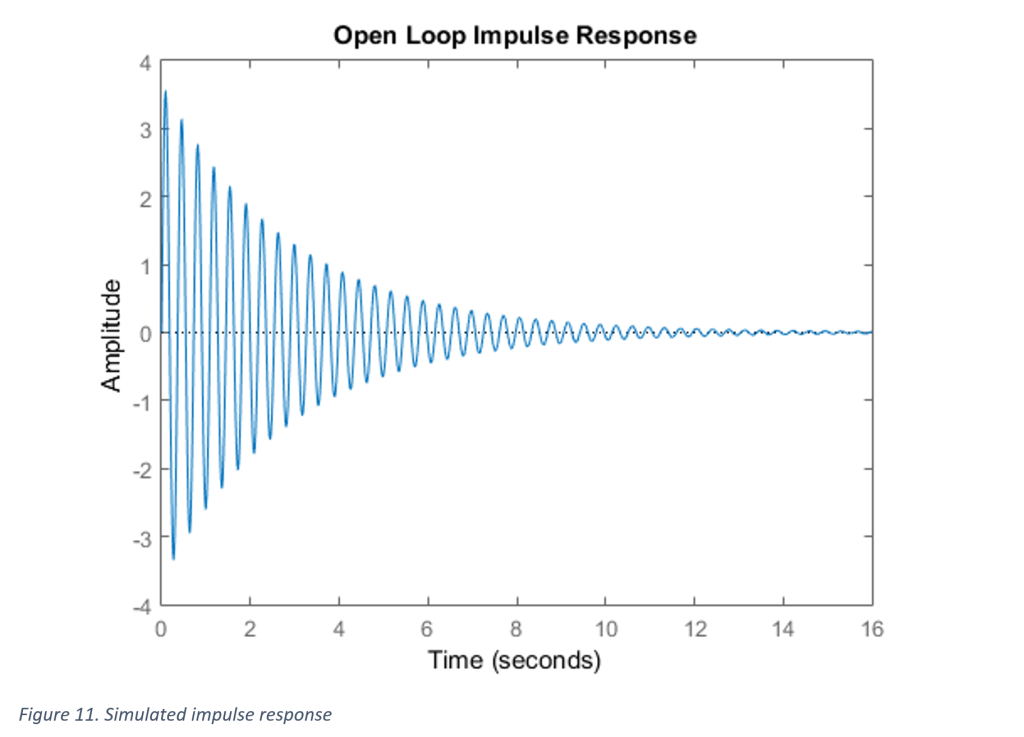
The original motor found in the stir plate is similar to those used to rotate a plate of food in a home microwave. It is an Autotrol permanent magnet synchronous AC gear motor.

These motors can be controlled only by varying the AC’s frequency or by changing their gear ratio, neither of which are cheap or ideal for this application.

The motor that will be used instead is a uni-polar stepper motor.

I chose to use a stepper motor given that stepper motors are inexpensive and do not require additional feedback components to achieve precise control. This particular stepper motor can provide up to 88.3 N·cm of holding torque which should be more than enough for this application.

To control the stepper motor, an A3967 Microstepping Stepper Motor Driver will be used. These guys can be easily implemented thanks to Brian Schmalz’s Easy Driver.

The Easy Driver is supplied with 6-30 volts and can be configured to deliver full steps or micro steps. It is designed to drive bi-polar stepper motors or uni-polar steppers wired as bi-polar. It can supply up to 700 mA to each phase.

A single step is achieved by sending a 3.3 V pulse to the Easy Driver. This particular stepper motor will complete one revolution every 200 steps, so a pulse frequency of 200 Hz correlates to a rotation of 1 revolution per second.

I found that the motor operated much more smoothly when the Easy Driver was configured to operate in micro step mode. Rather than taking a full step each pulse, the stepper motor will take an 8th of a step, or one revolution for every 1600 pulses. This scheme is ideal for microcontrollers that can deliver a pulse width modulation (PWM) signal.

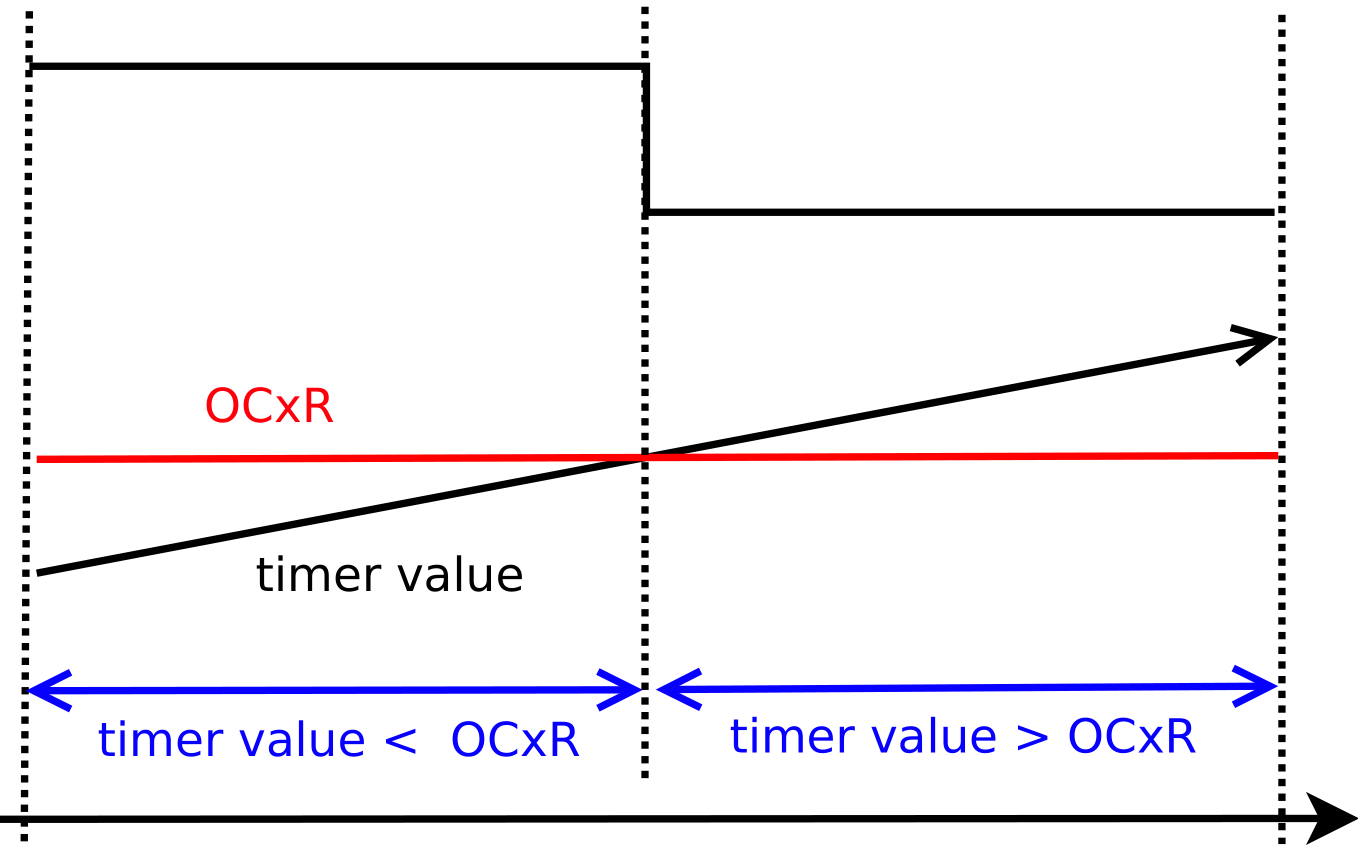
Two factors influence the PWM signal that is generated by the microcontroller: the period (how often a pulse is generated) and the duty cycle (the ratio of high to low within the period).

The period can be controlled using a hardware timer configured as an interrupt source. The period is set by assigning a value to the “period register”.

The duty cycle can be controlled by comparing the timer’s value with a threshold value known as the “output compare” value. If the counter’s value is less than the OC value, the designated pin will be driven high, if the counter’s value exceeds the OC value, the pin will be driven low.

By changing the values stored in the period register and the output compare register, the PWM’s frequency and duty cycle can be set. This is what will allow the user to precisely adjust the RPM of the stir plate. The duty cycle will be configured to always remain at 50%.

Power

Because stepper motors require direct current, an AC/DC converter will be required. To achieve the necessary DC voltage rails for this project, I will have to convert the 120 V_RMS AC coming from the wall to 12 V_DC and 3.3 V_DC. The 12 V_DC will come from a transformer/full-wave bridge rectifier, while the 3.3 V_DC will come from a linear LDO regulator that will cascade the rectifier.

To preserve the AC/DC converter and make it safer, I sealed it in many wrappings of electrical tape. I attached the grounding wire to the case and sanded down all of the contacts to deter current from passing through a human to earth ground in the event that the AC shorts to the case and someone were to touch it.

Now to verify the voltage rails…

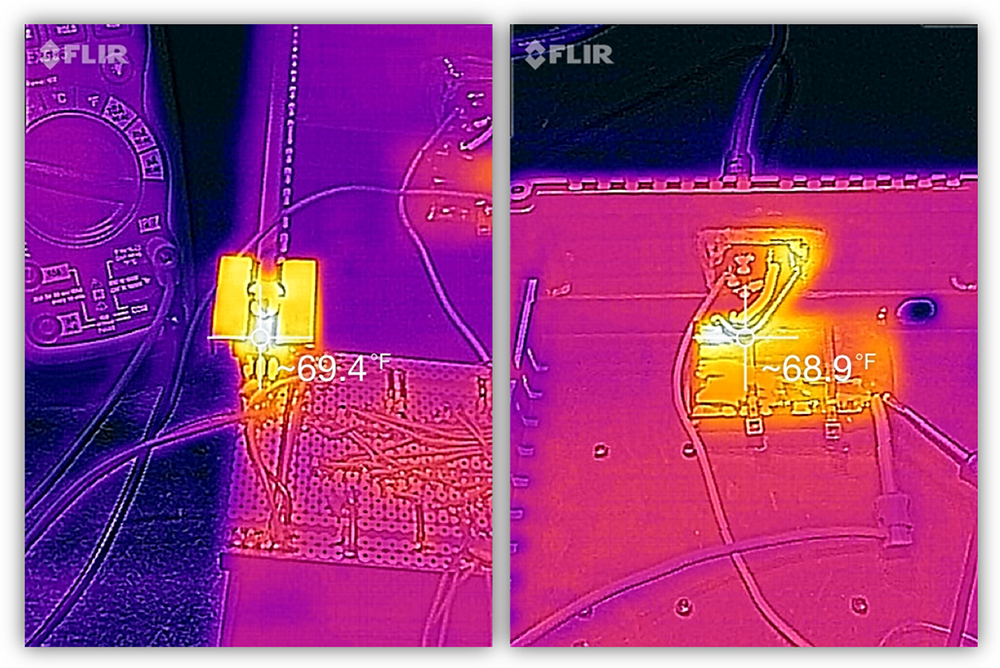
Great! 12.3 V @ 2 A for the stepper motor and 3.3 V @ 500 mA for the logic. The 3.3 V LDO is heat-sinked due to the fact that there is a 9 V voltage drop across it. To further verify that these PSUs are properly installed, I like to be sure there are no thermal issues under load.

Looks good.

Control Board

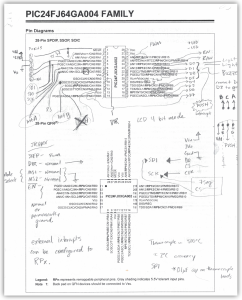
When implementing a controller into a project, I like to start by making a list of the I/O requirements (digital, analog, PWM, communication buses, etc…) and then comparing it to the controller’s datasheet to see if it meets the requirements of the project. In this case, I am just scratching out ideas on the PIC’s pin diagram.

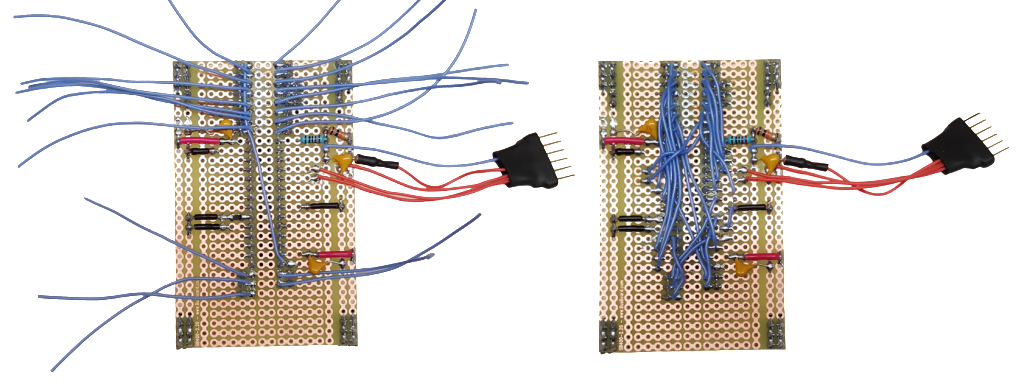
Looks like this will do… now to solder up some proto-board with the basic essentials for the controller. This will be the initial platform for development. To make things easier on myself, I added some female headers and grouped them in order by their function. I then labeled the picture to print out as a reference for wiring.

The proto-board is all wired and ready to begin coding with.

Thermocouple

To give the stir plate the ability to measure temperature, I will be adding a K-Type thermocouple with a MAX31855 thermocouple amplifier. This is similar to the thermocouple feature found on some multimeters.

The thermocouple is made up of two dissimilar metals that are joined at two ends. In the case of this K-Type thermocouple, the alloys are Chromel and Alumel. This arrangement will produce a measurable voltage when there is a difference in temperature between its hot junction (measurement) and cold junction (reference). Because this voltage differential is small, a thermocouple amplifier will be used.

The MAX31855 will take in the analog voltage from the thermocouple, amplify it, digitize it, and finally encode it. This information is then available via a SPI bus, so the only work I need to do is to write a driver that will grab these bits and decode them for the display.

The protocol is simple. Each time the slave select is pulled low, the temperature data is refreshed. There are 32 bits of information, however, only the 14 most significant bits contain the temperature data, the rest can be dismissed. The MSB is the sign bit, the next 11 bits contain the whole number, and the last 2 bits contain the fractional portion (allowing for increments of 0.25 °C).

For example, if the temperature were -121.5 °C, the data frame of the 14 most significant bits would look like this:

For storage, I added a tiny clothes pin to keep the thermocouple out of the way when it’s not being used.

User Interface

Display

The display that will be used in the user interface is a Hitachi HD44780 LCD. I am going to implement this in 4-bit mode, reducing the data pin requirements from 8 to 4 (this would have been a nightmare without a logic analyzer).

Now to come up with some kind of mounting bracket for the LCD. Here is the 3D model I generated in Blender and then printed on a Prusa i3.

LCD and bracket assembled and wired:

User interface fully assembled and painted:

Here are some of the menus that can be navigated to with the rotary encoder. The rotary encoder is interrupt driven, so navigation is seamless even if the microcontroller is busy with another process.

menuScroll

Rotary Encoder

A rotary encoder is essentially a device that consists of two or three switches. There are two switches that are either normally open or normally closed that will briefly change state each time the knob is rotated. The direction of the turn can be deduced by detecting which switch changed state first. The third switch allows the knob itself to act as a momentary push button. This single device can allow a user to scroll through and select different menu options.

Because mechanical switching is occurring as the rotary encoder is operated, debouncing each switch with passive low-pass filters will improve its overall function.

Audible Feedback Piezo Buzzer

Making an intuitive user interface is a challenge for any designer. It’s easy to navigate through something you designed, but the trick is to always stay in the mindset as if you were looking at it for the first time. Having haptic or audible feedback is a good way to let the user know that their input was received. Although the rotary encoder has distinguishable clicks, a piezo buzzer will generate an audible tone each time an input was successfully received.

Results

Final wiring:

Finished project:

Code

Buy me a coffee!

Blog

Heterogeneous Computing

December 19, 2015 Zack Goyetche

Introduction

As humanity continues to develop its technology, our reliance on digital information becomes more and more prominent. This digital information can manifest as a document of text, audio, images, videos, or bring life to a much more complex electro-mechanical system. It is the life blood of automation, it helps us fly our airplanes, maneuver our cars, and allows our economy and markets to function. We use this digital information for leisure and for work, and it’s hard to look around a home or work space today and not see its abundant presence.

At the heart of these different manifestations of digital information are streams of bits, zeros and ones. These bits are used to convey meaningful information. It must be this way due to the binary nature of the logic structures that allow digital computers to process information and make decisions. There are two big players in today’s methods of digital computing, general purpose processors and application specific digital circuits. The reason these two methods exist are because neither one is particularly good at doing what the other one does best.

A general purpose processor is excellent at making decisions and scheduling tasks. Its hardware is defined and so are the instructions it can interpret. It relies on a manmade program that resides in its memory, in which it is able to fetch the instructions from and perform the requested action. It is sequential in nature in that it must fetch an instruction, decode it, do the action requested (manipulate data), and proceed to the next instruction until the end of the program is reached. This method is desirable in that it makes it relatively easy to implement complex decision making trees which would otherwise require a very cumbersome finite state machine.

Application specific digital circuits are digital hardware that have been designed and optimized to perform one and only one task extremely well. It does not rely on instructions, rather, it is fed digital information at its input and a clock keeps cadence for the information as it propagates through the logic fabric towards the output. Because it does not need to fetch instructions in a sequential manner, there are many opportunities to pipeline certain processes and run multiple processes in parallel. For this reason, it is highly desirable to apply this method of computing to tasks that are computationally complex but redundant, such as encryption, image and video compression, software defined radio, wireless communication, networking, high frequency trading, and computer vision.

These circuits can be realized in a permanent optimized form, known as an ASIC (Application Specific Integrated Circuit), or as a malleable, re-configurable fabric known as an FPGA (Field Programmable Gate Array). While a general purpose processor and an ASIC/FPGA can do the same task, it is valuable to know when to employ one or the other, or both, as a solution for a project.

Xilinx ZYNQ 7000 SoC

The Xilinx ZYNQ could be considered a heterogeneous computer in that it combines both of the previously mentioned realizations of computing within a single package of silicon. This affords the designer the best of both worlds when dealing with systems that could benefit from the decision making abilities of a general purpose processor and the sheer computational power of application specific logic circuits. Within the Xilinx ZYNQ SoC is a hard processor consisting of two ARM Cortex A9 cores and a section dedicated to logic fabric much like what is found in a traditional FPGA. With this, the processing system (PS) can run bare metal or with an operating system, and is afforded the luxury of off-loading computationally intensive operations to hardware that is defined in the programmable logic (PL).

Here is a high level overview of the ZYNQ 7000’s architecture:

Programmable Logic

The programmable logic on the Zynq 7000 is available to extend the capabilities the processing system by hosting hardware accelerators or peripherals, which are commonly referred to as intellectual property (IP). It is connected to the PS with 9 AXI interfaces and over 3000 interconnections. The amount of programmable logic available is dependent upon the class of Zynq chip. Programmable logic, at a high level, is a matrix of resources connected to one another for a broad mesh of configurable interconnections. Within this matrix, various digital functions can be designed and implemented. The basic building block of these matrices are logic cells, each consisting of a 6 input look up table with dual flip flops. The Xilinx architecture also allows for these building blocks to also be turned into small distributed memory, shift registers, or other combinatorial functions.

Another resource within the PL are the DSP blocks. The DSP blocks are small but powerful MAC engines consisting of a 25×18 bit multiplier with a 25-bit pre-adder, followed by a 48-bit ALU and 96-bit accumulator. These blocks are intended for signal processing functions and filtering. Another important element of the PL is the block ram (BRAM). These are configurable 36 kb memory blocks can support memories from 1 bit up to 72-bits wide. They can be configured as single port or simple/true dual port memory. These blocks can be combined together to build larger memory or FIFOs. Lastly, the PL contains many clocking resources, such as mixed mode clock managers, PLLs, and regional and global clock buffers. The PL can be configured by use of an HDL (VHDL/Verilog), Vivado HLS (C/C++), Mathworks (MATLAB/Simulink), or LabVIEW.

Processing System

The processing system within the Zynq 7000 consists of a dual core ARM Cortex A9, each with their own L1 cache memory. On the 7020 device featured on the popular ZedBoard, the cores can be clocked up to 866 MHz and can support 128 I/Os. Additionally, it contains everything that is needed to run an operating system on a single core. Each core has its own NEON engine for multimedia applications and vector FPU engine for single and double precision. The cache currency between the two cores is controlled by the Snoop Control Unit. Both of the cores share 512KB of L2 cache and 256KB of on chip memory.

To complete the PS are standard peripherals such as interrupt controllers, timers, DMA, and debug. When the Zynq is initially powered, the processing system is the first to boot and will decide what will happen. The bit streams for the programmable logic can be stored on an SD card or within flash memory, and the PL fabric can be configured by the PS upon booting. Other key peripherals that are supported are USB 2.0, Gb Ethernet, SD/SDIO, CAN, I2C, I2S, SPI, UART, and XADC. The Zynq processing system can be implemented as bare metal (no OS), with an operating system, or both.

AXI Interface

In order for the PS to communicate with hardware peripherals that are instantiated within the PL, a communication protocol that allows for both the PS and PL to access the share information within DDR3 memory in a managed and timely manner must be implemented. This communication protocol is an industry standard known as AXI4 (Advanced eXtensible Interface 4). All of the IP blocks that are designed for a Zynq 7000 chip are created as AXI masters or slaves.

Three types of AXI can be implemented, namely, high performance memory mapped interface, lite memory-mapped interface, and stream interface. The stream interface is a reduced version of the memory mapped interface. The AXI master has the ability to initiates read and write commands, while the slave can only respond to these commands. The Xilinx AXI Interconnect IP contains a configurable number of AXI-compliant master and slave interfaces, and can be used to route transactions between one or more AXI masters and slaves.

In memory-mapped protocols, all transactions involve the concept of transferring a target address within a system memory space, where the IP operates in a defined memory map. For this reason, when implementing a hardware peripheral or accelerator, it must include the necessary I/O to allow it to join the AXI bus.

Software Design Tools

Xilinx provides a software package capable of managing every stage of design for the Zynq SoC. The Vivado Design Suite consists of three major components, namely Vivado, HLS (High-Level Synthesis), and SDK (Software Development Kit).

Vivado HLS

Vivado HLS is a software package that allows for IP to be implemented in C or C++. Traditionally, hardware is created using a hardware description language such as VHDL or Verilog. The advantage that HLS provides is that it allows the designer to describe the algorithm in a familiar manner using C/C++ which will then be automatically translated to VHDL or Verilog. There are further features within HLS that allows for loop and function optimization. A test bench for proving out the functionality of the hardware can also be developed in C or C++. With that being said, HLS’s easing of the development process comes at the expense of control.

There are applications where the designer cannot afford to have HLS do its work behind the curtains and must manually write the HDL. It should be noted that Vivado HLS will not accept just any C code. C code that attempts to allocate dynamic memory cannot be used in HLS, all memory instances must be static. Additionally, no system calls such as std or file I/O can be used, and recursive functions should be avoided. Additionally, the HDL that is generated by HLS will not as “readable” as if it were written by a human.

Vivado IP Integrator

Vivado IP integrator is used to define the PL and PS connections and interfaces in a way similar to what is found in Mathworks Simulink. A block diagram is created where all of the IP can be dropped into and connected with other IP cores or processing systems. Once the connections have been finalized, a high level HDL wrapper is created and used to generate a bit stream. Once the bit stream has been generated, the design moves over to Xilinx’s SDK.

Xilinx SDK

Xilinx SDK is used to program the ARM cores. As mentioned before, the ARM cores can run a bare metal application, an operating system, or both. Because the Zynq is a processing centric system, this is an absolutely crucial piece of the design process. The ARM cores can be programmed in C and have access to user customizable libraries and hardware drivers. The SDK IDE provides true homogenous and heterogeneous multi-processor design and debug capabilities.

Buy me a coffee!

Projects

AC Power Monitoring

November 16, 2015 Zack Goyetche 1 Comment

Here is a power monitor I designed featuring the Maxim 78615+LMU isolated energy monitoring IC. In conjunction with the Maxim 78700 analog to digital converter, it has the ability to make isolated power measurements from single or split phase AC with 4 kV of isolation. The transformer couples power to the ADC as well as providing a magnetic coupling for data transmission, allowing the microcontroller to be electrically isolated from the main AC line it is monitoring.

Using a 128×64 LCD, power information can be displayed in real time. Here is the power consumption of my laptop and monitor as I am typing this!

Board layout:

Schematic:

Documentation and tutorial coming soon…

Code

Buy me a coffee!

Projects

Teeter Totter Pt. 2 (Control)

October 25, 2015 Zack Goyetche 4 Comments

This is part two of a two part series… check out the construction and characterization of the teeter-totter in part one!

Buy me a coffee!

First things first, here are some results. These two GIFs show how a phase lead compensator can significantly improve a system’s ability to recover from outside disturbances. Keep scrolling down if you’re interested in how this was implemented!

Uncompensated impulse response:

Compensated impulse response:

Abstract – Previously, a teeter-totter was constructed and modeled in the continuous time domain. This model will be brought into the z-domain so that it can be controlled by a sampled data discrete time control system. A NI Data Acquisition Tool as well as an ARM Cortex-M4 will be used to implement the control schemes.

The first control system to be implemented is the open loop controller, allowing the system to reach a reference point with minimal overshoot and settling time, but still remaining vulnerable to disturbances.

To reject disturbances, a closed loop lead compensator will be implemented, allowing for rejection of disturbances, but contributing notable steady state error.

To get the best of both worlds, the lead compensator will be combined with the open loop controller to create a “Bridged-T” network. This will allow for low steady state error due to the open loop controller and rejection to disturbances due to the lead compensator. This control system will be implemented on an ARM Cortex M4 microprocessor rather than the NI-Data Acquisition tool used for the phase lead compensator.

The z-domain

Previously, a continuous time domain transfer function for the teeter-totter was arrived at by means of impulse response.

To bring this continuous time s-domain transfer function into the z-domain, the z-transform must be applied.

This z-domain model now takes into account a sample time of 18 ms and the zeroth-order hold to account for the data acquisition instruments.

Open Loop Control

Open loop control can be a desirable means of control for certain applications where disturbance rejection is not necessary. Additionally, open loop controllers can be applied in series with other methods of feedback control when it is desirable to reject disturbances to the plant. Open loop control is easy to implement and can allow a system to adjust to a reference point with little overshoot or steady state error, if any at all.

The following figure illustrates the implementation of an open loop controller F(z)

It can be seen that F(z) is a volt-to-volt transfer function, which explains the constant of 1/Ka out front. This allows the input to the system to be a reference position. The inverse of the actuator gain is used rather than the sensor gain due to the nature of the open loop system. Because there is no feedback present, it would be nonsensical to use sensor gain. Note the hat above Ka designating the experimentally determined numerical value that is a model of the true behavior of Ka.

The implementation of an open loop controller is simple. The idea is to create a transfer function based on the current (undesired) pole locations of the plant transfer function G(z), and the desired pole locations. By placing the undesired (actual) G(z) pole locations in F(z)’s numerator, they will effectively “cancel” out the undesirable poles. With that being said, the poles will never truly cancel out even though they may appear to be canceling mathematically. Finally, F(z)’s denominator is set to be the desired pole locations.

F(z)’s denominator can be anything, but the idea is to force the system to behave in a desirable way. Ideally, the poles of G(z) would be repeated on the positive real axis, as close to the imaginary axis as possible. It is likely that this will not be achievable, as it will require more actuator energy than what is available. It is for this reason that a happy medium must be arrived at, where the desired behavior is in harmony with the system and its resources.

The following three figures illustrate the step response of the system FG(z) and the controller F(z)

The simulation in Figure 3 shows the most ideal response characteristics, however, it would require an initial burst of over 100 V, which would exceed the limitations of the voltage supply and actuators.

The simulation in Figure 4 shows a response which requires little energy, and it can be seen that the system takes a significantly longer amount of time to reach steady state when compared to the response time in Figure 3.

The simulation in Figure 5 shows the ideal balance between response time and energy requirements. The initial “push” does not exceed the limitations of the actuators or the supply, and the amount of time to settle at steady state is reasonable (approximately half of a second).

Therefore, the transfer function of F(z) is set to be

The actual outputs of FG(z) and G(z) can be seen in the following figure

The pink line illustrates F(z)’s output, where it is coming from a DAC whose dynamic range is 0 to 5 volts. The blue line illustrates FG(z)’s output. Note the slight overshoot and settling time of approximately 0.5 seconds.

Uncompensated step response:

Compensated step response:

These GIFs demonstrate the reduction in settling time due to the open loop controller when the system is given the command to move to a new reference point.

Lead Compensation

Lead compensation is a type of compensation which improves the loop phase at the expense of the loop gain. Lead compensation is desirable in that it can be used to first stabilize the system with an acceptable phase margin before attempting to improve its performance. Lead compensators tend to speed up the transient response but will increase the steady state error. Additionally, lead compensation can increase system bandwidth and stability margins, and for this reason, is essential to systems that are unstable or on the border of instability.

The following figure illustrates the implementation of an lead compensator D(z)

Because D(z) is a volt-to-volt transfer function, the Ks hat term must be applied to the input reference. The hat on Ks denotes that it is a model of the sensor gain, not the physical gain exhibited by the sensor which is found in the feedback loop.

The approach for implementing a lead compensator can be done in either the time or frequency domain. The idea is to satisfy the specifications on phase margin, gain crossover frequency, and steady state accuracy. To achieve this, a Bode plot of the plant is constructed and the phase curve is adjusted in such a way that the phase margin and gain crossover frequency requirements are met.

A phase lead compensator consists of a single pole and zero. Its transfer function can be described as

Where a pole exists at z = 0 and a zero exists such that a < 1.

In order to properly implement a phase lead compensator, the pole and zero must be placed in a manner that the benefits of the positive phase shift are achieved and the magnitude degradation is accounted for. The following figures illustrate the magnitude and phase frequency characteristics of a phase lead compensator D(z), the plant G(z), and the combined system DG(z).

It can be seen in Figure 9 that the plant is unstable at the zero crossover frequency (the phase is less than -180°). Figure 8 illustrates a lead compensator which exhibits the phase lead required to stabilize the system, along with the undesirable but necessary degradation to the gain at lower frequencies. Figure 10 shows the combined result DG(z), where the system is now stable with approximately 65° of phase margin at the gain crossover frequency.

The transfer function for the lead compensator which resulted in these stability improvements is

The phase lead controller was implemented in a manner illustrated by Figure 7. The resulting controller and system outputs can be seen in the following figures.

Note that the system now has the ability to be adjusted to a reference point with some undesired transient characteristics and steady state error (Figure 11), but can respond to impulse responses and reject disturbances (Figure 12).

Note that the blue illustrates the system output and the pink illustrates the DAC output to the actuators.

Figure 12 shows a settling time improvement by a factor of 8. The system settles in approximately 1.5 seconds due to an impulse response, compared to the uncompensated system which settled in approximately 12 seconds.

Bridged-T Controller

The Bridged-T network is a style of compensation that utilizes the two previous methods of control in a way that harnesses the benefits of both methods. The idea is that the open loop controller will be used to “throw” the system to the desired location when a step response is seen at the input, and the lead compensator will take control only when there is an error signal present. In essence, the open loop controller does the heavy lifting and the lead compensator does the fine tuning once the system is in the ball-parked location. This style of control achieves better performance and accuracy than what could have been possibly using a traditional PID controller.

It can be seen in the diagram above that there are a few new elements introduced to the control scheme. There is a block M(z) and a feed forward path that contains the open loop controller. Additionally, there is a second summing junction after the lead compensator D(z). If there is no error signal present from the first summing junction, D(z) is effectively removed from the system (it has no effect), and the system will behave in a way such that its only form of control is coming from the open loop controller F(z).

If an error signal is present, it will be the result of the sensed position subtracted from (Ks)G(z)F(z). It is at this point in which the phase lead controller D(z) will correct any error in the system and provide disturbance rejection.

F(z) and D(z) are described by Equation 3 and Equation 5 respectively.

M(z) is described by the following transfer function

The following plots show the impulse and step response of the Bridged-T controlled system.

Note that the blue illustrates the system output and the pink illustrates the DAC output to the actuators.

Figure 14 shows improved transient and steady state error characteristics over the system which was previously controlled by only the lead compensator (Figure 11).

Figure 15 shows the system’s ability to still reject impulse disturbances. The system performs even better given (a settling time of approximately 600 ms, improvement factor of 20). This could be due to the fact that the control scheme was implemented in C code on an ARM Cortex M4 processor rather than with LabVIEW on the Agilent ADC/DAC tool.

Conclusion

After the teeter-totter was constructed, a model was derived by observation and applied to the prototypical second order system transfer function. This s-domain transfer function was brought into the z-domain by means of the z transform, only after the data acquisition characteristics had been corrected for by combining the zeroth order hold with the plant transfer function.

The first form of control that was examined was open loop control which provided the system with the ability to adjust to a reference point with little overshoot or steady state error, if any at all. The open loop controller was easy and quick to implement by examining where the undesired poles were located, “cancelling” them out, and introducing poles in locations that achieved the desired response.

The next form of control implemented was a form of feedback control known as phase lead compensation. The phase lead compensator consists of one pole and one zero such that the pole is less than the zero. Phase lead compensation was used not just to achieve stability, but to introduce a phase margin of nearly 65°. While the system was able to reject disturbances with a reasonable settling time, it lacked the DC gain and low steady state error of the open loop controller.

To get the best of both worlds, a “Bridged-T” compensator was implemented. This network combines the desired control effects exhibited by the two previous forms of control, one making up for what the other lacks. The open loop controller was used to “throw” the system to the desired location when a step response is seen at the input, and the lead compensator will take control only when there is an error signal present. In essence, the open loop controller was doing the heavy lifting and the lead compensator was fine tuning the system it was in the ball-parked location set by the open loop controller.

Out of my own curiosity, I implemented the Bridged-T controller in C code on an ARM Cortex-M4 to exercise the implementation of digital control systems on a microcontroller. The ARM Cortex-M4 proved to outperform the NI Data Acquisition tool. It decreased the settling by a factor of 20, up from the previous factor of 8 seen in the phase lead compensator.

Projects

Teeter Totter Pt. 1 (Construction & Characterization)

October 16, 2015 Zack Goyetche 1 Comment

This is part one of a two part series… check out the implementation of various control schemes in part two!

Buy me a coffee!

Abstract – A teeter totter will be constructed for the purpose of a sampled data control system demonstration. Upon completion of construction, the teeter totter and its sensor and actuator systems will be characterized to obtain a prototypical second order system transfer function. This model will then be used to design a controller and compensator for the system.

Construction

For this exercise, the system will be a teeter totter. It is of interest to construct a system that exhibits as little amount of non-linearities as possible. The goal is to characterize its response and develop a control system that will decrease the teeter totter’s settling time by a factor of 10. The teeter totter will consist of four main parts:

A plane which is free to move about an axis with one degree of freedom
A post to hold the axle and elevate the plane
A base to secure the post and actuators
A system of sensors to allow for position information of the plane’s angle

The following images are of the 3D models that were created using Blender to generate parts 1, 2, and 3 by means of 3D printing.

The final constructed teeter totter can be seen in the following image with annotated points of interest:

teeter_fig3fixed

The plane (1) has one degree of freedom of which it is free to rotate about the axis established by its axle (2). Skateboard ABEC-5 bearings are held in place by a hex bolt, two washers, and a nut. The bearings allow for a reduction of friction which will improve linearity. The axle post (3) attaches the plane and bearing assembly to the base (4). The permanent donut magnets (5, 6) are glued to a bolt which allows for fine elevation adjustments to be made. The sensor network is comprised of two infrared emitters (7) and a single infrared photo-diode (8). The sensor network was chosen to operate in the infrared spectrum so that the system would be impervious to ambient light. The actuator network is comprised of two electromagnets (9, 10) which operate together in an opposing fashion. Their magnetic fields will repel and attract the permanent magnets (5, 6) to actuate the plane.

The sensor network provides feedback to a controller which will then deliver control signals to the actuators. The infrared photo-diode will pass a current that is proportional to the amount of infrared light being received. This current is then converted to a voltage by passing it through a resistor to ground. The voltage is then correlated to the position of the plane.

The actuator network is wired in series. Its input comes from a push-pull network of complementary transistors. A current can be delivered to the base of the NPN/PNP transistor push-pull network by the controller, causing a current to flow in the desired direction through the coils in order to achieve the appropriate magnetic field orientation.

The following schematic describes the electrical setup of the sensors, actuators, ADC output and DAC input:

The connector (J3, J7) delivers power to the sensor network and converts the current to a voltage using an adjustable potentiometer. This voltage is then sent through a gain stage and an offset stage for conditioning to the ADC.

The actuator network (seen in Figure 5) works in a similar fashion, where the input form the DAC (J6) is conditioned by an offset stage and gain stage in order to deliver +/- 12V to the actuator coils.

A prototype was created which can be described by the previous schematics in Figures 4 and 5 (excluding voltage regulators) in addition to a printed circuit board.

Modeling

The sensor and actuator network was characterized in the following fashion: For the sensors, the plane of the teeter totter was manually positioned at various points and the corresponding output voltage was noted. For the actuators, an input voltage was delivered from -12 to +12 volts and the position of the teeter totter plane was noted. The results have been tabulated and can be seen in the following tables and plots.

teeter_fig7table2

From the results above, the data points have been characterized by the following linear equations

Sensors:

Actuators:

The absolute value of the slope from Equation 1 represents the sensor gain, Ks, and the absolute value of the slope from Equation 2 represents the actuator gain, Ka.

The system was then connected to an oscilloscope and power supply in order to obtain the impulse and step responses. The output voltages are obtained from the infrared sensors. They relate the position of the teeter totter’s plane to a voltage.

From Figure 9, twenty periods were used to find the average values of the period (T), damped frequency (ω_d), natural frequency (ω_n), time constant (τ), damping coefficient (σ), and damping ratio (ζ).

The following calculations are with regard to the impulse response:

The transfer function can now be constructed from the obtained values. The prototypical transfer function for a second order system is

In a similar fashion, the transfer function can be obtained using the step response:

The transfer function obtained from the step and impulse response can now be plotted using Matlab:

Conclusion

The teeter totter constructed is suitable for a sampled data control system demonstration. While in its current state it still exhibits some nonlinear characteristics, it should be sufficient for moving forward to the next phase. The system can continue to be improved upon as a controller and compensator is being developed for it.

The next step is to develop a discrete model for what is currently a continuous time model. Once this is achieved, a microprocessor will be able to read in sensor data through an analog-to-digital converter, make control decisions based on the control scheme and sampled data, and output the appropriate control signals through a digital-to-analog converter.

This is part one of a two part series… check out the implementation of various control schemes in part two!

Blog

Sampling Continuous Signals

September 24, 2015 Zack Goyetche

Introduction

Analyzing continuous signals by means of discrete methods requires special considerations in order for the results to be meaningful and accurate. Underlying this task is an exercise of optimization, where the capturing of continuous information must be in harmony with the constraints of the digital system. The goal is to spend the least amount of computational resources required to digitally represent a continuous signal.

Throughout this exercise, theory and principles that have arisen out of a half of a century of communication systems and signal processing study will be defined, applied, and demonstrated by example through computational software.

These principles include:

Bridging the analog and digital domain using the Nyquist-Shannon sampling theorem.

Representation of discrete signals in time and frequency domain using the Fast Fourier Transform algorithm.

Defining essential bandwidth using Parseval’s theorem.

Detecting energy signals by means of autocorrelation and ESD comparison (Fourier pairs).

It will be necessary to examine signals with domains in both time and frequency, as each domain gives access to different information contained within the signal.

The Fourier Transform is a technique for mapping a function between its time/frequency or space/wavenumber domains.

The Fourier Transform is defined as follows

In everyday human experience, the signals we perceive are essentially continuous. For example, the sound waves produced by an Opera singer or heat transfer between two objects are processes which can take on an infinite number of values and exist continuously in time. This is in opposition to discrete signals which exist as packets that can take on a finite number of values and are discontinuous.

With the advent of digital computation, scientists and engineers now have the ability to solve complex problems where closed form solutions do not exist or are too difficult to obtain. In order for a digital computer to perform computations on such problems, they must be done numerically rather than analytically. For this reason, a signal that is continuous must be broken down into discrete components in such a way that its essence is captured.

Sampling, as stated previously, is the process of breaking down a continuous signal into a numeric sequence. The Nyquist-Shannon sampling theorem states that [1]:

If a function x(t) contains no frequencies higher than cps (counts per second), it is completely determined by giving its ordinates at a series of points spaced 1/2B seconds apart.

A sufficient sample-rate is therefore 2B samples/second, or anything larger. Conversely, for a given sample rate (f_s) the band limit for perfect reconstruction is B ≤ f_s/2.

Oftentimes, it is only necessary to consider a certain range of frequencies within a signal. While a signal may theoretically have infinite bandwidth, nearly all of its energy is likely be contained within a finite bandwidth of frequencies – this frequency range is known as the essential bandwidth of a signal. To define the essential bandwidth of a signal, Parsevel’s theorem can be used to evaluate the amount of energy contained within a bound of frequencies [2].

Parseval’s theorem can be expressed as follows

What this implies is that the total energy contained within a time domain waveform summed across all time is equal to the total energy contained within that same signal’s frequency domain waveform summed across all frequencies. From this, an arbitrary variable B can be assigned to the bounds of the infinite sum and set equal to a percentage of the total energy of the signal. Using the fundamental theorem of calculus, a closed form solution can be found. Consider the following example where

The variable B can be solved for provided that the total energy E is known and |X(f)|² is integrable. Solving for B in the example above would provide the bandwidth necessary to capture 99% of the signal’s total energy. Alternatively, the essential bandwidth can also be solved for numerically by an iterative process.

Because signals can exist in one of two forms, power or energy, it may be of interest to establish the form of a given signal. It is known that for an energy signal, its energy spectral density (ESD) and autocorrelation functions form a Fourier pair. The ESD of a signal is defined as follows

And the autocorrelation of a signal is defined as follows

If the signal x(t) is an energy signal, the resulting Fourier pair exists such that

And vice-versa

Discretization of Continuous Signals

Consider the signal g₁(t) = Δ(t/2) . This signal is defined for all values of time.

To determine the necessary sampling rate for this signal, its essential bandwidth must be established. By taking the Fourier transform of this signal, the magnitude of its frequency components will become apparent.

It can be seen in Fig. 2 that the signal’s magnitude is significantly reduced at frequencies greater than 0.5 hertz and less than -0.5 hertz.

To determine this signal’s essential bandwidth, the signal’s total energy must be must be found for all frequencies.

The total energy of this signal can be found by integrating the square of the frequency components over all frequencies. From Equations (3) and (8)

It is desired to capture 99% of this signal’s energy, so by assigning a variable to the limits of integration and setting the integral equal to 0.99 times the total energy, the essential bandwidth can be found.

From this result, the Nyquist-Shannon sampling theorem suggests that a sampling frequency as low as 0.65 samples per second can be used. Because this frequency is extremely low relative to the number of instructions a modern processor can handle per second, a modest sampling frequency of 4 samples per second will be used for the following simulations.

The discrete versions of this signal at a sample rate of four samples per second can be seen in Fig. 3 and Fig. 4.

The autocorrelation function compares a time domain signal with a shifted version of itself. The resulting function is defined in Equation (5).

Performing autocorrelation on the discrete signal g₁(t) results in the following time domain waveform

Given that g₁(t) is an energy signal, the same discrete waveform should result from taking the inverse FFT of its ESD function. The ESD function is defined in Equation (4).

Performing the inverse FFT on ψ_g₁(f) results in the following time domain waveform

It can be seen in Fig. 5 and Fig. 6 that g₁’s autocorrelation function R_g₁(τ) and ESD function ψ_g₁(f) are indeed Fourier pairs.

Next, consider the signal g₂(t) = ∏(t) . This signal is defined for all values of time.

Like in the previous example, performing a Fourier transform on this signal will reveal the magnitudes of the frequency components across all frequencies.

It can be seen in Fig. 8 that the magnitude of G₂(f)’s frequency components do not diminish as quickly as G₁(f) did.

To find the total energy of this signal, the square of the frequency components are integrated over all frequencies. From Equations (3) and (11)

To stay consistent with the previous signal g₁(t), a sampling frequency of 4 samples per second will also be used for g2(t), as it exceeds the f_s ≥ 2B rule established by the Nyquist-Shannon sampling theorem. The discrete versions of this signal can be seen in Fig. 9 and Fig. 10.

Performing autocorrelation on the discrete signal g₂(t) results in the following time domain waveform

Performing the inverse FFT on ψ_G2(f) results in the following time domain waveform

Because g₂(t) is also an energy signal, the autocorrelation function R_g2(τ) and ψ_G2(f) are Fourier pairs, as illustrated by Fig. 11 and Fig. 12.

Now, let us consider the system shown in Fig. 13.

The blocks labeled H₁(f) and H₂(f) are ideal low pass filters with a bandwidth of 2 hertz.

The discrete frequency representation of the filters can be seen in the following figures

Passing the signal G₁(f) through the ideal LPF H₁(f) results in the following discrete waveform

Performing an inverse FFT on the signal Y₁(f) = G₁(f)H₁(f) results in the following signal y₁(t)

Reconstructed in this fashion, it can be seen that the signals g₁(t) [Fig. 3] and y₁(t) [Fig. 17] are remarkably similar even with all frequency components greater than/less than 2 hertz removed from y₁(t).

Passing the signal G₂(f) through the ideal LPF H₂(f) results in the following discrete waveform

Performing an inverse FFT on the signal Y₂(f) = G₂(f)H₂(f) results in the following signal y₂(t)

Unlike the previous example with g₁(t) and y₁(t), it is evident that there are some imperfections resulting from the reconstruction of y₂(t). This could be due to the fact that the ideal low-pass filter with a bandwidth of 2 hertz was not able to capture the signal in its entirety. Signals that exhibit abrupt changes in time, such as the changes that occur around the corners of the rectangular function, require higher frequency (energy) components. Filtering out these components will produce smoother and more oscillatory like behaviors in such areas.

Mixing y₁(t) with y₂(t) results in the signal y(t). The following figures illustrate both time and frequency domains of the final signal

Conclusion

In order to effectively process continuous signals on a digital system, the signal bandwidth must be known. By applying the Nyquist-Shannon sampling theorem and Parseval’s theorem, the essential bandwidth of a signal can be defined and a sampling rate can be chosen. Choosing a sample rate that is too high will unnecessarily increase the demands on the processor and amount of memory required, while choosing a sample rate too low will result in loss of information and aliasing.

There is more to the story, however! Check out ‘What Nyquist Didn’t Say‘ by Tim Wescott.

Appendix

Matlab Code used in this project

Link to Github

Scaling issues with MATLAB’s FFT function

It should be noted to the reader that the FFT function contained within the MATLAB software requires special attention when attempting to properly scale in both time and frequency.

When performing an FFT, it is necessary to first perform an FFT Shift with the FFT of the desired signal inside its argument. For example

G1 = fftshift(fft(g1));

When attempting to plot a function in the frequency domain that resulted from a time domain function, such as the one above, the magnitude of the signal must be scaled down by a factor of the sampling frequency. For example

fs_g2 = 4; %sampling frequency for g2
normalize_g2 = fs_g2; %normalizing factor
G2_scaled = (G2)/normalize_g2; %divide G2 by normalizing factor

References

[1] “Communication in the presence of noise”, Proc. Institute of Radio Engineers, vol. 37, no. 1, pp. 10–21, Jan. 1949.

[2] Parseval des Chênes, Marc-Antoine “Mémoire sur les séries et sur l’intégration complète d’une équation aux différences partielles linéaire du second ordre, à coefficients constants” presented before the Académie des Sciences (Paris) on 5 April 1799.

Buy me a coffee!

Blog

SMD Soldering 101

Video August 25, 2015 Zack Goyetche 3 Comments

I’ve created a YouTube video that shares some tips and techniques I’ve picked up for SMD soldering.

Watch the whole video:

If you want the condensed version, scroll down for brief explanations and animations!

Soldering a 32 pin microcontroller with solder paste and hot air:

Watch this section in real time!

When soldering a package that has many pins, it is advantageous to use solder paste and hot air, as many pins can be soldered at the same time. While this method may create bridging or leave some connections unsoldered, applying flux and dragging an iron slowly across all of the pins is usually enough to fix any issues. As always, clean up the left over flux with 99% isopropyl alcohol or naphtha.

Soldering a 24 pin TQFN package with solder paste and hot air:

Watch this section in real time!

When you have pads that are entirely covered by the part package, or even mostly covered, your only choice is to reflow with hot air or an oven. The approach is similar to the previous example, however, you should take extra care to ensure your connections are aren’t shorted given that you cannot visually inspect them. You can ohm out the pins with a multimeter before applying power to be sure that you won’t damage your part.

Soldering a 10 pin MSOP package with an iron:

Watch this section in real time!

For packages that don’t have a tremendous amount of pins, you may just want to use your iron and solder. In this demonstration I am soldering pin by pin. There are other techniques with an iron that involve pre-loading the tip with solder and steadily dragging across the pins. This method is fast and efficient, but requires special soldering iron tips such as this one: T15-CF4

Soldering 0603 resistors and capacitors:

Watch this section in real time!

Soldering SMD resistors, capacitors, and inductors can also be done with an iron or paste/hot air. When soldering with an iron, you want to apply solder to one pad and let it cool. Grab your part with tweezers and then liquefy the solder again with the iron as you use your other hand to slide the part over the pad. Once the solder cools again, remove the tweezers and your part should be held in place. You can now apply solder to the other side of the part to finish the connection.

Buy me a coffee!

Blog

Automate Your Test Bench

August 24, 2015 Zack Goyetche 2 Comments

Why automate tests?
Automating tests on your bench is beneficial for a number of reasons:

You can collect more data in less time.
Mitigate human error.
Real-time data processing.
Data can be organized and exported in predefined formats.
Free up time to work on another part of the project or take a break.

How can I automate my tests?
First, you need instrumentation that is programmable. Your instrument is programmable if there is a communication port on it that allows for at least one way data transmission. There are a variety of software tools available to send and collect data from them, both free and paid.

In industry, it is common for companies to use National Instrument’s LabVIEW, Keysight’s VEE, or even Matlab for writing test automation programs. LabVIEW and VEE are both graphical programming languages specifically designed for automated testing, measurements, data analysis, and reporting. Matlab is most commonly found in academia, however, you will sometimes find Matlab in companies who have a lot of legacy code.

You don’t need expensive software to automate your own tests at home (or at work for that matter). Any programming language that can send and receive data through your USB or RS232 port will suffice, however, some are better than others.

Python is a powerful language that lends itself to this sort of task. There is a python library called ‘PyVisa’ which allows you to easily communicate with programmable instruments by use of the NI VISA drivers. Using the PyVisa library in conjunction with NumPy, SciPy, MatPlotLib, and OpenPyXl offers a very powerful tool for gathering and processing data obtained from programmable test equipment. If your instrument operates off of a non-ASCII text based protocol, such as Modbus, you can use the pySerial library to send and receive each byte, and even find yourself a CRC algorithm already written for you in python!

What is VISA?
VISA stands for Virtual Instrument Software Architecture. It is a standard developed by National Instruments for configuring, programming, and troubleshooting instrumentation. It can interface by means of USB, Ethernet, Serial, GPIB, VXI, or PXI. The NI VISA drivers are free to download and use with your programmable instrument, even if you are not using NI LabVIEW.

Okay… I’ve heard enough. How about an example?
Let’s say you have just designed an amplifier circuit and you want to characterize its amplitude response for a range of input frequencies.

Easy.

You can write a python script that utilizes the instruments’ SCPI commands to systematically characterize the amplifier’s gain for a given range of input frequencies.

SCPI stands for Standard Commands for Programmable Instruments. It is a standard by which instruments can communicate with a computer using ASCII text strings. Most instruments today use this standard and will come with a programming manual that tells you all of the SCPI commands that the instrument understands when it is put into ‘remote’ mode.

For this example, I will be using the following equipment:

Click on each of the instruments to see the python functions I have written for them. The function prototypes can be found here.

Note that if you happen to have the same instruments as me and would like to use my code, you may have to change the resource name for your instrument:

I have written a script that will output the resource names for all of your connected instruments. It can be found here on my github page.

Here is an example of what the output might look like when you run the script:

For this test, I will need to be able to remotely carry out the following functionalities:

Set power supply voltage
Set power supply over current protection
Toggle power supply channels on/off
Set waveform generator amplitude and frequency
Toggle waveform generator channel on/off
Measure peak to peak voltages from both channels of the oscilloscope

Once all of these have been written in, I can call these functions sequentially in the test script just as if I were preforming the task by hand.

The test script for characterizing the gain of the amplifier can be found here.

To summarize what will happen in this test:

Over current protection is set and the amplifier is given power from two channels of the power supply.
The amplitude of the input signal is set to 4 mV and the frequency is set to 1 Hz.
A peak-to-peak voltage measurement is taken by the oscilloscope of both the input and output signals of the amplifier.
The frequency is increased by 100 Hz, and the input and output peak-to-peak voltage is measured again.
This process is repeated until the frequency of the input signal has reached 1 MHz.
Once the test has been completed, the raw data is automatically exported into an Excel file in addition to generating a scaled plot with a title and axis labels and then saving this plot as a PDF file. The auto-generated plot is so that I can easily visualize the data to see if what I collected is meaningful.
Turn off the power supply and waveform generator’s outputs.

It should also be noted that calculations can be performed on the data as it is collected. In this example, I am calculating the gain in dB after each input and output peak-to-peak voltage reading is taken, and then storing the result in an array.

Here is what the auto-generated plot looks like:

I now have an idea of what my data looks like and every data point has been saved into an Excel spreadsheet. Now I can do what ever I want with the data — create more plots, add trend lines, etc…

Conclusion
Test automation is a valuable skill to have in your tool belt. If you are a designer, chances are you are going to be spending a lot of time validating your design requirements. While the programming requires a significant amount of effort in the front end, you will surely save time in the long run and become a more capable designer and tester.

Buy me a coffee!

Projects

TIG Pulse Welding with Due

May 4, 2015 Zack Goyetche 8 Comments

Here is a project that utilizes the 12-bit DAC on the Arduino Due to deliver open-loop control signals to a TIG welder. A DC TIG welder will normally deliver a constant current arc, but by hi-jacking the foot pedal input, a pulse frequency can be set and the arc can switch between a peak and background current.

Pulsing the TIG arc is beneficial cosmetically and will reduce the amount of heat input.

Code

Schematic, documentation, and demo to come…

Projects

LEDs & Bandpass Filters

May 4, 2015 Zack Goyetche 2 Comments

http://www.youtube.com/watch?v=BZ9rNsvkRDA

An addressable RGB LED strip with 7 bandpass filters.

63Hz – Dark Red
160Hz – Red
400Hz – Orange
1kHz – Yellow
2.5KHz – Green
6.25kHz – Blue
16kHz – Indigo

Code

Schematic and documentation to come…

Case

Motor

Power

Control Board

Thermocouple

User Interface

Display

Rotary Encoder

Audible Feedback Piezo Buzzer

Results

Introduction

Xilinx ZYNQ 7000 SoC

Programmable Logic

Processing System

AXI Interface

Software Design Tools

Vivado HLS

Vivado IP Integrator

Xilinx SDK

Board layout:

Schematic:

Uncompensated impulse response:

Compensated impulse response:

The z-domain

Open Loop Control

Uncompensated step response:

Compensated step response:

Lead Compensation

Bridged-T Controller

Conclusion

Construction

Modeling

Conclusion

Introduction

Discretization of Continuous Signals

Conclusion

Appendix

Matlab Code used in this project

Scaling issues with MATLAB’s FFT function

References

Watch the whole video:

Soldering a 32 pin microcontroller with solder paste and hot air:

Soldering a 24 pin TQFN package with solder paste and hot air:

Soldering a 10 pin MSOP package with an iron:

Soldering 0603 resistors and capacitors:

Est. 2014